Equações Diferenciais Exatas

RELEMBRANDO: diferencial total (dF) de uma função  
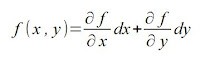
Por exemplo: f(x, y) = x² + 3xy nos dá df = (2x + 3y) dx + 3x dy.
Agora voltando.
Definição: uma EDO escrita na forma M(x, y) dx + N(x, y) dy é exata se o formato mostrado (em vermelho) for o diferencial total de uma função f(x, y).

Exemplo: a equação x²y³ dx + x³y² dy = 0 é exata pois é a diferencial total da função f(x, y) = ⅓ x³y³

Critério para determinar se uma função é exata: considere uma EDO na forma M(x, y) dx + N(x, y) dy = 0. Se a ED é exata, temos . Teremos também  , logo   porque as derivadas parciais mistas são iguais.

Exemplo: verifique se 2xy dx + (x² - 1)dy = 0 é exata.
Temos:   M = 2xy   e   N = x²-1. Derivando parcialmente como mostrado acima, temos ambas as derivadas parciais mistas iguais a 2x. Portanto, a ED é exata.

Formato da solução numa ED exata: temos M(x, y) dx + N(x, y) dy = 0. Se a ED for exata, podemos descrevê-la como df = 0, portanto f(x, y) = C é a solução da ED.

1. Verificar se a ED é exata ✓
2. 
   o termo g(y) aparece na função porque sabemos apenas a parte originária da derivada parcial de x
3. 
4. x²-g'(y) = x²-1   =>   g'(y) = -1   =>   g(y) = -y
5. f(x, y) = x²y - y. Solução: x¹y - y = C