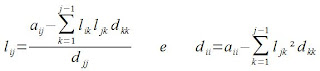Decomposição por LDLT

Seja A uma matriz simétrica. Podemos decompor A pelo produto de 3 outras matrizes a saber. L é uma matriz triangular inferior e unitária e D é uma matriz diagonal. A solução é: [Ly = b; Dt = y; L^Tx = t] para  .
Podemos ver que um termo usa o outro pra ser definido (l usa d e vice versa). Por isso tem uma ordem para fazer: d₁₁, l₂₁, l₃₁, d₂₂, l₃₂, d₃₃ (num exemplo de matriz de ordem 3). A ordem é essa porque fazendo o d₁₁ (esse é o primeiro em matriz de qualquer ordem) é possível descobrir todos os l da primeira coluna (ou seja, abaixo do índice 11, já que a matriz é triangular inferior e unitária). Após descobrir todos esses, com o d₂₂ dá pra descobrir todos os l abaixo de 22 e por aí vai.