Equações lineares de 1ª ordem

São equações do tipo , onde:
- y e dy/dx são multiplicados por funções de x, somente;
- y e dy/dx estão elevados a 1

Método de resolução:

1. resolva a ED na forma descrita acima para a forma padrão   dividindo a equação por a₁(x)
2. procurar um fator de integração μ(x) multiplicando a ED na forma padrão por μ(x):
    , implicando que 
   SENDO QUE μ(x) é obtido de 
   
   

Muito confuso, né? Pois é. Sóoo que eu tenho exemplo!

Resolva 

1. Colocar no formato padrão (dividindo por x): 
2. Obter um μ(x): 
3. Multiplicar a ED por μ(x):
4. Encontrando y: 
   

Somatórios e exemplos

Conceito de OPERAÇÃO RELEVANTE: A op. relevante é a operação básica mais importante do código que representa seu custo. Numa inicialização de vetor, por exemplo, a operação relevante é a atribuição. Em geral, a op. relevante tem a ver com a semântica (significado; função) do código.
A complexidade do algoritmo muitas vezes é representada pela op. relevante pelo fato dessa representação muitas vezes ser da mesma ordem de complexidade do total de operações.

Somatórios simples:

1. soma de uma constante: 
   
   
2. soma dos nºs naturais até n: 

Exemplos:

1. análise da função fatorial

   int fatorial (int N) {       int fat = 1;       for (in i=2; i<=N; i++)          fat = fat * i;       return fat;    }

   Operação relevante: multiplicação f(n) = nº de repetições da OP. relevante

   
   
2. soma de matrizes
   
   

   for(int i=1; i<=N; i++)       for(int j=1; i<=N; j++)          C[i][j] = A[i][j] + B[i][j]

   Operação relevante: soma f(n) = nº de repetições da OP. relevante

   
   
3. multiplicação de matrizes
   
   

   for(int i=1; i<=N; i++)       for(int j=1; i<=N; j++){          C[i][j] = 0;          for(int k=1; k<=N; k++)             C[i][j] = C[i][j] + A[i][k] * B[k][j];       }

   Operação relevante: multiplicação f(n) = nº de repetições da OP. relevante

   
   
4. dois laços em sequência
   

   int soma = 0;    for(int i=1; i<=N; i++)       scanf("%d", &a[i]);    for(int j=1; i<=N; j++)       soma = soma + a[j];

   f(n) = nº de instruções

Análises de casos

Temos 3 casos possíveis ao executar um algoritmo: melhor caso, pior caso e caso médio ou esperado.

O melhor caso é a execução com o menor número possível de instruções (ou seja, a mais eficiente).

O pior caso é a execução com o maior número possível de instruções (menos eficiente). Fornece um 'teto' para o número de instruções.

O caso médio é a média ponderada de todas as entradas e suas chances de ocorrer.

Os casos são causados por comandos condicionais, porque estes direcionam a caminhos diferentes de execução e esses caminhos podem ter mais ou menos comandos. Alguns exemplos pra entender direitinho:

Busca pelo maior elemento (entrada:vetor; saída: índice do maior elemento):

- num vetor de n elementos, são executadas n-1 comparações. Afinal, nunca saberemos se um número é o maior se não testarmos todos.

- num vetor de n elementos, podem ser executadas entre 1 e n atribuições (do índice do maior elemento pra variável que for retornar). Considerando o nº de atribuições:

• melhor caso: o elemento está na primeira posição
• pior caso: o elemento está na última posição
• caso médio: o elemento está no meio

Busca pelo maior E menor elementos (entrada:vetor; saída: índices do maior e menor elementos):

1. utilizando o seguinte método:
   if (a[i] > max) max = i;
   if (a[i] < min) min = i;
   - num vetor de n elementos, são executadas 2n-2 comparações. Afinal, nunca saberemos se um número é o maior ou menor se não testarmos todos.
2. utilizando o seguinte método, que faz muito mais sentido porque se um elemento é maior, ele não pode ser o menor, nem precisa conferir:if (a[i] > max) max = i;else if (a[i] < min) min = i;

• melhor caso: n-1 comparações com o maior elemento na primeira posição
• pior caso: 2n-2 comparações com o maior elemento na última
• caso médio: supondo 50% de chance de o elemento ser maior que o anterior e não entrar no else e 50% de chance dele não ser maior que o anterior e entrar, temos o seguinte: f(n) = ((n-1) + (2n-2)) / 2 = 3/2 (n-1) comparações em média

Algoritmo de busca sequencial de um elemento no vetor:

- o elemento pode existir ou não, e a análise de complexidade é feita separadamente para essas duas hipóteses.

- a busca é sequencial, ou seja, vai procurando no vetor até achar ou chegar no fim, indicando que não achou o elemento procurado.

• pesquisa sem sucesso: são feitas n comparações para constatar que o elemento não esta lá.
• pesquisa com sucesso:
• melhor caso: o elemento está na primeira posição (1 comparação)
• pior caso: o elemento está na última (n comparações)
• caso médio: média ponderada dos casos e suas probabilidades. Como não sabemos probabilidades específicas, podemos considerar todas iguais (p = 1/n). Assim, temos f(n) = 1/n (1 + 2 + 3 + ... + n), resultando em (n+1)/2

Análise de espaço e tempo

A análise de complexidade dos algoritmos é importante para definir o custo inerente a eles. Desta forma, dado um problema pode-se definir qual é a melhor solução para ele. Todo tipo de custo é calculado, mas os principais são o tempo de execução (uso de CPU) - relacionado ao nº de operações que o programa executa - e o espaço ocupado (uso de memória) - relacionado à quantidade de dados.
A análise do espaço é feita de forma muito simples: avaliando a quantidade de variáveis e o espaço ocupado por cada uma delas. O uso eficiente do espaço se dá quando o algoritmo utiliza o espaço da entrada mais uma fração desse valor. O uso pouco eficiente se dá quando o algoritmo utiliza o espaço dos dados da entrada mais uma vez ou mais esse valor.

A análise do tempo pode ser feita de duas formas:

• Medição empírica: mede o tempo do mesmo algoritmo para entradas diferentes. É uma medição muito particular, porque vai depender da capacidade de processamento do computador, do hardware, do sistema operacional, enfim. Muitas coisas. Por ser uma medida tão particular, ela só é válida para o ambiente em que foi feita, apesar de dar o tempo real da execução.
• Medida analítica: determina a quantidade de trabalho para resolver o problema baseando-se na entrada de dados, no algoritmo utilizado e na natureza do problema. O tempo é proporcional à quantidade de instruções executadas (dentre atribuições, operações lógicas, aritméticas, leitura e escrita de dados, condicionais, loops, chamadas a outras funções e combinações de todos esses procedimentos), portanto, conta-se o número de instruções e o custo é dado por uma expressão matemática que tem n (nº de entradas) como parâmetro e resulta no nº de instruções em função de n. Para medir certinho o tempo, basta calcular o tempo médio por instrução e multiplicar pelo nº de instruções.
  
  Exemplo: seja o comando for(i=0; i<N; i++) a[i] = 0; O laço é executado N vezes. Portanto, há 1 atribuição de valor a i (em i=0), N incrementos de i, N+1 comparações para ver se i<N e N atribuições do valor 0 a cada posição do vetor a. Portanto, a inicialização de um vetor é dada por f(n) = 3n + 2; sendo f(n) o número de instruções executadas.

DADO: um computador de 1GHz executa aproximadamente 10^9 instruções por segundo, cada uma com custo médio de 1ns.

Algoritmo ótimo é aquele que cujo custo equivale ao custo mínimo da classe de problemas que ele resolve.

AEDS - Primeiros conceitos

Algoritmo é um conjunto finito (preferencialmente pequeno) de instruções destinadas a solucionar determinado problema. Há uma definição formal de algoritmos chamada Máquia de Turing. Todo algoritmo pode ser expresso por uma MT que, em resumo, é uma máquina que interpreta uma sequência de bits - uma abstração do computador.
Características desejáveis em algoritmos:

• Correção: o algoritmo apresenta a saída correta para qualquer entrada válida
• Eficiência: uso eficiente dos recursos computacionais
• Elegância: ser simples e claro, de fácil interpretação
• Robustez: ser capaz de lidar com qualquer entrada de dados
• Generalidade: ser adaptável a dados e sistemas diferentes

Estrutura de dados é a abstração de um conjunto de dados, sua representação. A escolha da estrutura de dados correta é importantíssima, pois ela limita ou define quais algoritmos usar. Algoritmos e estruturas de dados são interdependentes, e juntos compõem programas.

O problema que o algoritmo visa solucionar é o que fazer com uma entrada para que ela gere a saída desejada; é a relação entre entrada e saída. O algoritmo especifica como fazer isso com a entrada.

Computabilidade é a existência de uma solução algorítmica para um problema. Por exemplo, achar o enésimo termo da sequência de Fibonacci é um problema computável, mas achar o segredo da felicidade não (profundo, hein). Toda função computável pode ser expressa por uma MT.

Teoria de algoritmos é uma área que trata da eficiência dos algoritmos. As soluções para problemas computáveis são uma fração de todos os problemas, e soluções eficientes são uma fração destas. 

Equações Diferenciais Exatas

RELEMBRANDO: diferencial total (dF) de uma função  
Por exemplo: f(x, y) = x² + 3xy nos dá df = (2x + 3y) dx + 3x dy.
Agora voltando.
Definição: uma EDO escrita na forma M(x, y) dx + N(x, y) dy é exata se o formato mostrado (em vermelho) for o diferencial total de uma função f(x, y).

Exemplo: a equação x²y³ dx + x³y² dy = 0 é exata pois é a diferencial total da função f(x, y) = ⅓ x³y³

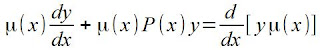
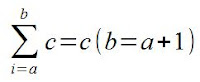
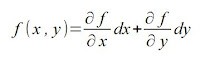
Critério para determinar se uma função é exata: considere uma EDO na forma M(x, y) dx + N(x, y) dy = 0. Se a ED é exata, temos . Teremos também  , logo   porque as derivadas parciais mistas são iguais.

Exemplo: verifique se 2xy dx + (x² - 1)dy = 0 é exata.
Temos:   M = 2xy   e   N = x²-1. Derivando parcialmente como mostrado acima, temos ambas as derivadas parciais mistas iguais a 2x. Portanto, a ED é exata.

Formato da solução numa ED exata: temos M(x, y) dx + N(x, y) dy = 0. Se a ED for exata, podemos descrevê-la como df = 0, portanto f(x, y) = C é a solução da ED.

1. Verificar se a ED é exata ✓
2. 
   o termo g(y) aparece na função porque sabemos apenas a parte originária da derivada parcial de x
3. 
4. x²-g'(y) = x²-1   =>   g'(y) = -1   =>   g(y) = -y
5. f(x, y) = x²y - y. Solução: x¹y - y = C

Tabela de Integrais

Segue a "breve" tabela de integrais do livro de cálculo do Thomas, vol. 2:

Exercício resolvido - EDO de primeira ordem com valor inicial

Resolva


Resolução:

Fim!
Agora, só pra mostrar o processo inverso: demonstre que x² + y² = 25 é solução da ED acima (dy/dx = -x/y).

Derivando x² + y² = 25 implicitamente em relação a x, teremos

EDOs de primeira ordem

Para começar, uma Equação Diferencial Ordinária é a equação das derivadas de uma função desconhecida de uma variável. Fica confuso assim, mas com o exemplo melhora.

Método das equações separadas: uma EDO de primeira ordem pode ser descrita como 

Que resulta em:

• g(y) dy = h(x) dx      => y e x separados
• consequentemente,

Pooor exemplo: Resolva (1 + x) dy - y dx = 0

Comentários:

• a solução de uma EDO da forma F(x, y, y') = 0 é uma família de curvas do tipo G(x, y, C) = 0, que depende do parâmetro arbitrário C
• a solução G(x, y, C) = 0 é chamada de solução geral da ED
• quando o valor de C é determinado através de condições iniciais, a solução é chamada de solução particular da ED

Colocando isso no exemplo acima (cada reta do gráfico é uma solução particular):

Decomposição pelo método de Cholesky (LLT)

Seja A uma matriz simétrica e definida positiva (ou seja, para a determinante de A - λI todos os λ devem ser maiores que 0)(ou seja, mais fácil ainda: é simétrica e tem a diagonal principal toda positiva). Podemos decompor A por um produto de duas outras matrizes (L e a transposta de L), em que L é triangular inferior e LT é triangular superior. Para obter L, realizamos as seguintes operações:

Feito isso, temos as duas matrizes. IMPORTANTE: a conta é feita coluna por coluna, não adianta tentar começar pela diagonal que não vai dar. Agora um exemplo, de praxe:

Lindo (só que não)! Agora só falta resolver o sisteminha em vermelho aí em cima. Vão dar números horrorosos, então é bacana cortar com 4 casas decimais. Não pretendo resolver, preguiça.

Decomposição LU com pivotação parcial

A pivotação parcial é como se fosse uma 'extensão' do método LU. Existe pra lidar com o pivô nulo. Caso o pivô seja 0, tem que trocar as linhas E o termo independente do resultado do sistema linear que gerou a matriz A. O pivô deve ser o maior número EM MÓDULO da coluna (independentemente do primeiro elemento ser 0). Pra lidar com essa troca de forma facilitada, trabalha-se com uma matriz permutação P, do tipo identidade. A cada troca efetuada no dispositivo prático, troca-se também a ordem das linhas da matriz P e dos multiplicadores e o resultado de LU passa a ser PA, e não apenas A. Vamos ao desenho de exemplo:

Agora resta só montar as matrizes L e U e resolver o sistema:

Decomposição de matrizes (LU)

A decomposição de matrizes LU é um método de resolver sistemas que permite um resultado mais refinado, digamos assim, e nos permite calcular a margem de erro desse resultado. Pra muitas matrizes, escalonar seria a forma mais fácil, mas nem sempre a mais precisa. A forma de resolver o sistema com decomposição se chama Dispositivo Prático. Fica mais fácil explicar o passo a passo com um exemplo:

Sobre o desenho acima, que eu esqueci de colocar e agora to com preguiça de fazer outro: o vetor transposto resultado do sistema se chama b. b = [1, 2, 3] nesse sistema. Vamos usar isso lá em baixo. Agora voltando.
A matriz A vai ser decomposta em duas matrizes: L e U. A matriz L é triangular inferior unitária e U é triangular superior.

O dispositivo prático serve para descobrir os números que faltam nas matrizes L e U para que o produto delas seja a matriz A. Depois de decompor, tem que resolver outros sistemas (Ly = b e Ux = y), mas por enquanto vamos ficar nesse aqui. O dispositivo se parece com uma tabela. O primeiro passo é colocar a matriz lá e numerar as linhas:

Feito isso, devemos começar o procedimento definindo um pivô da primeira coluna. O pivô é o primeiro elemento, de cima pra baixo, e deve ser diferente de 0. Ele é usado para calcular multiplicadores que irão zerar o resto da coluna, como no processo de escalonamento mesmo. Após zerar essa primeira coluna, eis o que temos:

Ok, zeramos a primeira coluna. Agora, seguindo o modelo do escalonamento, temos que zerar a segunda (precisamente, a posição 3x2, ou seja, o 1/3 da linha 5). Pra fazer isso, definimos o pivô pra essa coluna e repetimos o procedimento.

Prontinho! Agora devem estar se perguntando qual o objetivo disso. É simples: os multiplicadores que descobrimos são os elementos das posições correspondentes na matriz L e as linhas (nesse exemplo) 1, 4 e 6 formam a matriz U. Assim temos

Pronto. Agora lembra do Ly = b e Ux = y? São os dois sistemas abaixo (lembrar do b lá de cima, resultado do primeiro sistema):

Taí, a resposta do primeiro sistema marcada em azul!
Agora só falta o cálculo do erro (que nesse sistema vai dar 0 porque só temos números bonitinhos):
















Como eu disse, nesse exemplo o erro é 0. Mas trabalhando com números decimais, provavelmente ele será maior que 0. E o negócio do módulo do máximo valor é tipo assim: vamos supor que r = [-4, 2, 3] => o erro será 4 (módulo máximo). Fim!

Funções de Várias Variáveis - parte 1

Funções de Duas Variáveis
Citando o livro, "Os domínios de funções reais de duas variáveis reais são conjuntos de pares ordenados de números reais, e as imagens são conjuntos de números reais do tipo que usamos até agora." Ou seja, uma função no modelo z = f (x, y) tem x e y como o par ordenado de variáveis que resulta num número z. O par (x, y) está no domínio D e o número z está no conjunto imagem.
O livro cita algo importante, que é dar às suas variáveis nomes (letras) que lembrem o que elas são. Afinal, duvido que alguém descubra que T = é a fórmula de distância entre dois pontos se eu não avisar.

Domínios e Imagens
Domínio: maior conjunto possível que gere como resultado um número real.
Imagem: conjunto de valores gerados pela aplicação da fórmula no domínio.
Seguinte: vamos evitar entradas que levem a números complexos ou divisão por 0. Então, na hora de definir o domínio de uma função que mantenha sua imagem dentro dos números, tem que prestar atenção se tem uma divisão, uma raiz, essas coisas. Exemplo:

Função	Domínio	Imagem
w = raiz(y - x²)	y ≥ x² pra não dar raiz de negativo	[0, ∞)
w = 1/x*y	x * y ≠ 0	(-∞, 0) U (0, +∞)
w = sen xy	plano xy	[-1, 1]

Pontos de fronteira, interiores, espaço aberto e fechado, regiões limitadas e ilimitadas
Nossa. Eu custei a conseguir enfiar isso na cabeça. O livro define pontos interiores e de fronteira da seguinte forma: "Um ponto (x, y) em uma região (conjunto) R no plano xy é um ponto interior de R se é o centro de um disco que está inteiramente em R. Um ponto (x, y) é um ponto de fronteira de R se todo disco centrado em (x, y) contém ao mesmo tempo pontos que estão em R e do lado de fora de R. (O ponto de fronteira propriamente dito não precisa pertencer a R.)" - acho bem confuso, ainda mais depois de falar que o ponto de fronteira não precisa pertencer a R... Mas com imagens acredito que dê pra entender.
Sobre as regiões, uma região é aberta se só contém pontos interiores, e fechada se contém todos os seus pontos de fronteira. Eis a figurinha do livro:

Nessa figura dá pra entender porque tem inequação e equação, daí pensando na igualdade pra definir uma fronteira e na desigualdade porque os números são infinitos dá pra pegar. Mas assim, espero que seja isso mesmo.

PS: a região pode ser nem aberta nem fechada. Por exemplo, se forem colocados alguns pontos de fronteira no primeiro círculo acima (não pergunte como), a região não vai ser aberta nem totalmente fechada, pelas definições.

Por fim, "Uma região no plano é limitada se está dentro de um disco de raio fixo. Caso contrário é não limitada".