segunda-feira, 11 de novembro de 2013
Teste da razão e da raiz
Me justificando, se tá ali pronto e simples, não vejo porque eu ter que digitar as fórmulas no programinha de fórmulas. É muito chato e trabalhoso.
Testes da comparação
Teorema: Seja Σ an e Σ bn séries de termos não negativos; Se Σ an é convergente e an > bn para qualquer n, então Σ bn também é convergente. Se Σ an é divergente e an < bn , Σ bn é divergente.
Exemplo do livro estou realmente preguiçosa hoje.
Ok, agora o próximo:
Exemplo do livro estou realmente preguiçosa hoje.
Ok, agora o próximo:
Marcadores:
4º período,
calculo,
cálculo,
cálculo 4,
cálculo IV,
calculo-iv,
comparação no limite,
convergência,
divergência,
séries convergentes,
séries divergentes,
séries infinitas,
teste da comparação
Série P
Série P é toda série cuja variável n tem uma potência fixa p, que é um número real. O "formato" da n-ésima variável é sempre 1/np. A série P irá convergir se p > 1 e divergir se p <= 1. Um exemplo retirado do livro:
(eu ainda não peguei qual é a do fundo cinza)
(eu ainda não peguei qual é a do fundo cinza)
domingo, 10 de novembro de 2013
Teste da integral
Teorema: Seja Σ∞n = 0 an uma série de termos positivos, então se ∫0∞ f(x) dx existe e der um valor "fixo", a série é convergente. Se o resultado for ∞, a série é divergente.
A série de termos positivos só converge se e somente se as somas parciais de seus termos tiverem um limite superior.
Exemplos:
A série de termos positivos só converge se e somente se as somas parciais de seus termos tiverem um limite superior.
Exemplos:
- Série harmônica:
Observe que o limite dessa série dá 0, mas ela é divergente. Isso ocorre porque não há um limite superior para as somas dos seus elementos. Ou seja, citando o livro porque eu nem entendi isso muito bem, "a soma dos 2n termos terminados em 1/2n+1 é maior do que 2n/2n+1 = 1/2". 1/2 no caso é o limite superior das somas dos termos. - Série convergente qualquer:
Marcadores:
4º período,
calculo,
cálculo,
cálculo 4,
cálculo IV,
calculo-iv,
convergência,
divergência,
integral,
série,
séries convergentes,
séries divergentes,
séries infinitas,
teste da integral
Séries telescópicas
Série telescópica é engraçadinha, porque a soma é sempre 1. Normalmente são resolvidas com frações parciais (lembra de cálculo 1? Pois é, eu também não lembrava). Exemplim:
(não sei porque minhas imagens estão ficando com fundo cinza, que saco)
(não sei porque minhas imagens estão ficando com fundo cinza, que saco)
Teste do n-ésimo termo para convergência
- Se uma série é convergente, então an tende a 0. Se o limite de an não for 0 ou não existir, a série é divergente. Em notação matemática:
- Sejam
séries convergentes.
Marcadores:
4º período,
calculo,
cálculo,
cálculo 4,
cálculo IV,
calculo-iv,
convergência,
divergência,
séries convergentes,
séries divergentes,
teorema,
teste do n-ésimo termo
Séries geométricas
 Considerações sobre séries geométricas:
Considerações sobre séries geométricas:- elas sempre começam de n = 0
- a é uma constante diferente de 0 e r é a base
- fim
Séries infinitas
Citando o senhor Thomas, "dada uma sequência de números {an}, uma expressão da forma a1 + a2 + a3 + ... + an + ... é uma série infinita." Do próprio nome "série infinita" já dá pra tirar alguma coisa, né. Normalmente as séries são definidas por somatórios (é bem melhor do que escrever um monte de termos soltos).
Séries infinitas podem ser classificadas como convergentes ou divergentes.
Uma série convergente é aquela cuja soma resulta num número (calma, não julguem o sentido dessa frase ainda), por exemplo: 1 + 1/2 + 1/4 + 1/8 + ... + 1/2n = 2. Mas obviamente a gente não precisa somar infinitos termos pra chegar nesse resultado: quando se soma até o n-ésimo termo (a chamada n-ésima soma parcial) já dá pra ir percebendo mais ou menos onde a série vai dar.
Já uma série divergente é aquela cuja soma tende ao infinito (infinito não é número).
Séries infinitas podem ser classificadas como convergentes ou divergentes.
Uma série convergente é aquela cuja soma resulta num número (calma, não julguem o sentido dessa frase ainda), por exemplo: 1 + 1/2 + 1/4 + 1/8 + ... + 1/2n = 2. Mas obviamente a gente não precisa somar infinitos termos pra chegar nesse resultado: quando se soma até o n-ésimo termo (a chamada n-ésima soma parcial) já dá pra ir percebendo mais ou menos onde a série vai dar.
Já uma série divergente é aquela cuja soma tende ao infinito (infinito não é número).
Marcadores:
4º período,
calculo,
cálculo,
cálculo 4,
cálculo IV,
calculo-iv,
convergência,
divergência,
série,
séries convergentes,
séries divergentes,
séries infinitas
domingo, 11 de agosto de 2013
Paradigmas de projeto de algoritmos
Um paradigma é um conjunto de práticas que definem os modos de fazer de uma disciplina científica durante um certo período de tempo. Um paradigma é definido por:
– o que é para ser observado e avaliado
– as questões que devem ser feitas acerca de um tema de pesquisa
– como essas questões são estruturadas
– como os resultados das investigações científicas devem ser analisados
Em computação, do ponto de vista estrutural existem paradigmas racionalistas (tem origem na teoria da computação), tecnocráticos (origem na engenharia de software) e científicos (origem na teoria de algoritmos).
Existem, também, paradigmas de linguagens: orientadas a objetos, procedurais, lógicas, etc.
Alguns paradigmas de projeto de algoritmos:
● Recursividade: chama a si mesmo, direta ou indiretamente
● Tentativa e erro – backtracking: decompor o processo em um número finito de subtarefas que devem ser exploradas exaustivamente. Backtracking: selecione um caminho que pode levar à solução; se a escolha não se mostrar adequada então os caminhos derivados daquela escolha são ignorados e a busca pela solução retorna a um estágio anterior (backtracking)
● Divisão e conquista: Consiste em dividir o problema em partes menores, encontrar
soluções para as partes, e combiná-las em uma solução global
● Balanceamento
● Programação dinâmica: Se o mesmo subproblema precisa ser resolvido muitas vezes, então a abordagem é resolvê-lo uma vez e armazenar sua solução para uso posterior
● Algoritmos gulosos: Fazem a escolha que parece ser a melhor no momento
● Algoritmos aproximados
● Programação paralela
– o que é para ser observado e avaliado
– as questões que devem ser feitas acerca de um tema de pesquisa
– como essas questões são estruturadas
– como os resultados das investigações científicas devem ser analisados
Em computação, do ponto de vista estrutural existem paradigmas racionalistas (tem origem na teoria da computação), tecnocráticos (origem na engenharia de software) e científicos (origem na teoria de algoritmos).
Existem, também, paradigmas de linguagens: orientadas a objetos, procedurais, lógicas, etc.
Alguns paradigmas de projeto de algoritmos:
● Recursividade: chama a si mesmo, direta ou indiretamente
● Tentativa e erro – backtracking: decompor o processo em um número finito de subtarefas que devem ser exploradas exaustivamente. Backtracking: selecione um caminho que pode levar à solução; se a escolha não se mostrar adequada então os caminhos derivados daquela escolha são ignorados e a busca pela solução retorna a um estágio anterior (backtracking)
● Divisão e conquista: Consiste em dividir o problema em partes menores, encontrar
soluções para as partes, e combiná-las em uma solução global
● Balanceamento
● Programação dinâmica: Se o mesmo subproblema precisa ser resolvido muitas vezes, então a abordagem é resolvê-lo uma vez e armazenar sua solução para uso posterior
● Algoritmos gulosos: Fazem a escolha que parece ser a melhor no momento
● Algoritmos aproximados
● Programação paralela
Hashing
Hashing é uma técnica de busca para encontrar elementos a partir de uma chave em um grande conjunto previamente armazenado.
Essa técnica se baseia em criar tabelas e utilizar funções de transformações de chaves de forma a obter o índice do elemento na tabela. Podem ocorrer elementos com índice igual. Essas 'colisões' podem ser tratadas com listas encadeadas ou com encadeamento aberto, que será explicado mais adiante.
Tratamento de colisões:
As colisões podem ser tratadas por meio de listas encadeadas, ou seja, caso um elemento tenha um índice onde já há outro elemento, ele é inserido logo após a raíz da lista e aponta para o elemento seguinte.
Podem, também, ser tratadas por endereçamento aberto:
Essa técnica se baseia em criar tabelas e utilizar funções de transformações de chaves de forma a obter o índice do elemento na tabela. Podem ocorrer elementos com índice igual. Essas 'colisões' podem ser tratadas com listas encadeadas ou com encadeamento aberto, que será explicado mais adiante.
Como fazer uma tabela hash
a tabela tem um tamanho fixo M. Basta calcular, usando uma função hash, um índice para cada chave de forma a distribuí-los na tabela entre 0 e M-1.Tratamento de colisões:
As colisões podem ser tratadas por meio de listas encadeadas, ou seja, caso um elemento tenha um índice onde já há outro elemento, ele é inserido logo após a raíz da lista e aponta para o elemento seguinte.
Podem, também, ser tratadas por endereçamento aberto:
- Hashing linear: caso o índice definido para um elemento já esteja ocupado, ele será inserido na primeira posição vazia disponível a partir daquele índice. Só que é perigoso a tabela encher e os registros começarem a se agrupar.
- Hashing quadrático: o elemento é inserido na posição correspondente ao quadrado do primeiro índice encontrado.
- Hashing duplo: caso haja colisão, é aplicada outra função hash para obter outro índice.
Função hash:
A função hash mais comum para chaves inteiras é chave % M. Lembrando que caracteres podem ser transformados em inteiros utilizando seu código ascii.
Outros métodos de ordenação
Além dos métodos de ordenação interna vistos anteriormente, ainda existem outros que devem ser ressaltados. Normalmente, são melhores para conjuntos específicos de dados.
Ordenação digital: é adequada para conjuntos específicos de dados, como por exemplo CEP, porque tem o mesmo número de dígitos e seguem uma distribuição uniforme. Numa central de correios, por exemplo, as cartas poderiam ser separadas primeiro pelo primeiro dígito do CEP, e dentro dessa separação, pelo segundo dígito e assim por diante. Alguns algoritmos: radixsort, bucketsort.
Counting sort: ordenar um conjunto de N letras:
Contar as frequências de cada letra usando a chave como índice
Calcular a frequência acumulada
Ordenar no array temporário
Copiar no array original
Esse eu nem entendi muito bem, admito.
Ordenação parcial: ordenar parcialmente é pegar apenas os k primeiros registros de um conjunto de tamanho n em ordem. Mas esses k primeiros são ordenados de acordo com o total, só que depois deles o resto pode ficar tudo desordenado que não tem problema, a gente só queria os primeiros k mesmo.
Ordenação externa: a ordenação externa é efetuada quando o conjunto a ser ordenado não cabe na memória interna. São muito difíceis e exigem cuidado, pois o acesso a dados na memória externa é extremamente custoso e é apenas sequencial. Portanto, a complexidade é analisada de acordo com o número de transferências de dados entre memória externa ou secundária e a interna. Isso faz com que os métodos de ordenação externa variem de acordo com a tecnologia atual.
O método mais eficiente é a ordenação por intercalação. O algoritmo pega blocos de dados na memória externa, os ordena na memória interna e intercala esses blocos, fazendo várias passadas pelo arquivo. Eles são cada vez maiores, até que todo o arquivo esteja ordenado. To com preguiça de descrever o método das fitas, porque exige um exemplo. Caso um dia alguém precise, basta perguntar.
Ordenação digital: é adequada para conjuntos específicos de dados, como por exemplo CEP, porque tem o mesmo número de dígitos e seguem uma distribuição uniforme. Numa central de correios, por exemplo, as cartas poderiam ser separadas primeiro pelo primeiro dígito do CEP, e dentro dessa separação, pelo segundo dígito e assim por diante. Alguns algoritmos: radixsort, bucketsort.
Counting sort: ordenar um conjunto de N letras:
Contar as frequências de cada letra usando a chave como índice
Calcular a frequência acumulada
Ordenar no array temporário
Copiar no array original
Esse eu nem entendi muito bem, admito.
Ordenação parcial: ordenar parcialmente é pegar apenas os k primeiros registros de um conjunto de tamanho n em ordem. Mas esses k primeiros são ordenados de acordo com o total, só que depois deles o resto pode ficar tudo desordenado que não tem problema, a gente só queria os primeiros k mesmo.
Ordenação externa: a ordenação externa é efetuada quando o conjunto a ser ordenado não cabe na memória interna. São muito difíceis e exigem cuidado, pois o acesso a dados na memória externa é extremamente custoso e é apenas sequencial. Portanto, a complexidade é analisada de acordo com o número de transferências de dados entre memória externa ou secundária e a interna. Isso faz com que os métodos de ordenação externa variem de acordo com a tecnologia atual.
O método mais eficiente é a ordenação por intercalação. O algoritmo pega blocos de dados na memória externa, os ordena na memória interna e intercala esses blocos, fazendo várias passadas pelo arquivo. Eles são cada vez maiores, até que todo o arquivo esteja ordenado. To com preguiça de descrever o método das fitas, porque exige um exemplo. Caso um dia alguém precise, basta perguntar.
Algoritmos de ordenação eficientes
Algoritmos de ordenação eficientes são mais recomendados para arquivos muito grandes porque - adivinha - eles são eficientes. Tem 4 algoritmos eficientes: Quicksort, Shellsort, Heapsort e Mergesort.
Quicksort: o quicksort é baseado no bubble sort - ou seja, realiza trocas. Dado um conjunto inicial de dados, é escolhido aleatoriamente um índice cujo conteúdo será chamado pivô. Feita essa escolha, um contador i é iniciado do início para o fim, percorrendo os valores e comparando-os com o pivô. Ao achar um elemento maior ou igual ao pivô, o íncide i para e inicia-se um j, do fim para o início, percorrendo os valores e procurando um menor ou igual ao pivô. Quando esse elemento é encontrado, os valores das posições i e j são trocados e o processo recomeça. Quando os contadores i e j se cruzam (ou seja, i aponta para uma posição à direita de j), são definidas duas partições do vetor e são feitas duas chamadas recursivas do quicksort, uma para cada partição. Antes de prosseguir, note que ao formar partições, todos os elementos de uma delas serão menores ou iguais ao pivô e, da outra, maiores ou iguais ao mesmo.
O tempo de execução do algoritmo depende do bom balanceamento das partições, ou seja, se o número de elementos está bem distribuído dos dois lados do pivô. No caso de um bom balanceamento, o algoritmo é O(n logn). Porém, para o pior caso, o algoritmo é quadrático, o que o torna inviável devido às chamadas recursivas.
Shellsort: o shellsort é um melhoramento do insertion sort. Ele analisa o vetor como uma intercalação de conjuntos e ordena cada um desses conjuntos com o insertion sort. Uma vez ordenados, o processo se repete com conjuntos maiores e, para isso, menos espaçados. Explicando melhor, o shellsort faz passadas pelo vetor analisando elementos equidistantes entre si, com uma distância h dada por uma expressão no início do algoritmo. Ao ordenar os subconjuntos, que são formados por elementos com distância h entre si, o h diminui. Assim, os subconjuntos incluirão mais e diversificados elementos. O processo se repete até que h seja 1, ou seja, elementos adjacentes. O h=1 caracteriza o insertion sort, que é sensível à ordenação parcial do vetor e, portanto, muito eficiente.
Não existe análise de complexidade definida para o shellsort, porque o resultado depende da sequência h escolhida. Para algumas sequências, o algoritmo pode ser O(n^3/2), O(n^7/6), O(n^1,25) ou O(n*(log(n))2), como sugerem alguns experimentos.
Heapsort: o heapsort é um algoritmo baseado no selection sort. Ele organiza o vetor de forma que o elemento dos índices 2k e 2k+1 são sempre menores do que o do índice k. Fica mais fácil visualizar essa estrutura em forma de árvore, em que um elemento tem dois filhos e cada filho tem outros dois filhos e por aí vai. O pai sempre é maior que os filhos. Para montar o heap, inicia-se da metade do vetor (afinal, daí pra frente já não haverão mais filhos) e, para cada elemento, é selecionado o maior filho e comparado com o pai. Caso o maior filho seja maior do que o pai, os dois são trocados. Quando é analisado um elemento cujos filhos tem filhos e é feita uma troca, a análise segue a cadeia de filhos até o final para que o heap se mantenha correto. Quando ele estiver finalmente montado, o elemento da primeira posição é trocado com o da última e, como o atual topo é menor, o heap é corrigido. Ao final da correção, o mesmo é feito, porém com a penúltima posição e por aí vai, até sobrar apenas a posição do topo e aí o vetor estará o ordenado.
O algoritmo tem custo total da construção do heap e da ordenação, totalizando O(n log2n).
Mergesort: o mergesort é um algoritmo baseado em intercalação. Dado um vetor de tamanho n, ele vai separando em vetores menores cujo tamanho é metade do vetor anterior e por aí vai, até que cada vetor tenha tamanho 1. Em seguida, vai juntando pares de vetores intercalando-os de maneira ordenada. É um algoritmo recursivo. Como usa espaço extra, é aconselhado para situações de mesclar dois vetores já ordenados, por exemplo.
Tem custo O(nlogn) e usa espaço extra de tamanho proporcional a n para todos os casos (insensível a ordenação inicial do vetor).
Quicksort: o quicksort é baseado no bubble sort - ou seja, realiza trocas. Dado um conjunto inicial de dados, é escolhido aleatoriamente um índice cujo conteúdo será chamado pivô. Feita essa escolha, um contador i é iniciado do início para o fim, percorrendo os valores e comparando-os com o pivô. Ao achar um elemento maior ou igual ao pivô, o íncide i para e inicia-se um j, do fim para o início, percorrendo os valores e procurando um menor ou igual ao pivô. Quando esse elemento é encontrado, os valores das posições i e j são trocados e o processo recomeça. Quando os contadores i e j se cruzam (ou seja, i aponta para uma posição à direita de j), são definidas duas partições do vetor e são feitas duas chamadas recursivas do quicksort, uma para cada partição. Antes de prosseguir, note que ao formar partições, todos os elementos de uma delas serão menores ou iguais ao pivô e, da outra, maiores ou iguais ao mesmo.
O tempo de execução do algoritmo depende do bom balanceamento das partições, ou seja, se o número de elementos está bem distribuído dos dois lados do pivô. No caso de um bom balanceamento, o algoritmo é O(n logn). Porém, para o pior caso, o algoritmo é quadrático, o que o torna inviável devido às chamadas recursivas.
Shellsort: o shellsort é um melhoramento do insertion sort. Ele analisa o vetor como uma intercalação de conjuntos e ordena cada um desses conjuntos com o insertion sort. Uma vez ordenados, o processo se repete com conjuntos maiores e, para isso, menos espaçados. Explicando melhor, o shellsort faz passadas pelo vetor analisando elementos equidistantes entre si, com uma distância h dada por uma expressão no início do algoritmo. Ao ordenar os subconjuntos, que são formados por elementos com distância h entre si, o h diminui. Assim, os subconjuntos incluirão mais e diversificados elementos. O processo se repete até que h seja 1, ou seja, elementos adjacentes. O h=1 caracteriza o insertion sort, que é sensível à ordenação parcial do vetor e, portanto, muito eficiente.
Não existe análise de complexidade definida para o shellsort, porque o resultado depende da sequência h escolhida. Para algumas sequências, o algoritmo pode ser O(n^3/2), O(n^7/6), O(n^1,25) ou O(n*(log(n))2), como sugerem alguns experimentos.
Heapsort: o heapsort é um algoritmo baseado no selection sort. Ele organiza o vetor de forma que o elemento dos índices 2k e 2k+1 são sempre menores do que o do índice k. Fica mais fácil visualizar essa estrutura em forma de árvore, em que um elemento tem dois filhos e cada filho tem outros dois filhos e por aí vai. O pai sempre é maior que os filhos. Para montar o heap, inicia-se da metade do vetor (afinal, daí pra frente já não haverão mais filhos) e, para cada elemento, é selecionado o maior filho e comparado com o pai. Caso o maior filho seja maior do que o pai, os dois são trocados. Quando é analisado um elemento cujos filhos tem filhos e é feita uma troca, a análise segue a cadeia de filhos até o final para que o heap se mantenha correto. Quando ele estiver finalmente montado, o elemento da primeira posição é trocado com o da última e, como o atual topo é menor, o heap é corrigido. Ao final da correção, o mesmo é feito, porém com a penúltima posição e por aí vai, até sobrar apenas a posição do topo e aí o vetor estará o ordenado.
O algoritmo tem custo total da construção do heap e da ordenação, totalizando O(n log2n).
Mergesort: o mergesort é um algoritmo baseado em intercalação. Dado um vetor de tamanho n, ele vai separando em vetores menores cujo tamanho é metade do vetor anterior e por aí vai, até que cada vetor tenha tamanho 1. Em seguida, vai juntando pares de vetores intercalando-os de maneira ordenada. É um algoritmo recursivo. Como usa espaço extra, é aconselhado para situações de mesclar dois vetores já ordenados, por exemplo.
Tem custo O(nlogn) e usa espaço extra de tamanho proporcional a n para todos os casos (insensível a ordenação inicial do vetor).
sábado, 10 de agosto de 2013
Algoritmos de ordenação simples
Temos 4 algoritmos básicos de ordenação simples: Bubble Sort, Insertion Sort, Selection Sort e Enumeration Sort.
Bubble Sort: o bubble é um algoritmo baseado em trocas. Ele percorre o vetor do início ao final comparando pares de elementos e trocando-os caso seja necessário. Ele faz isso quantas vezes forem necessárias até que a ordenação esteja completa. A cada passada, o maior elemento analisado já fica no lugar.
O bubble sempre será O(n²) comparações. Para trocas, seu melhor caso é O(1), pois não faz trocas caso os elementos já estejam ordenados, e caso médio e pior caso são O(n²).
É um algoritmo amplamente utilizado didaticamente, porém é ineficiente.
Insertion Sort: o insertion analisa cada elemento e o insere na posição correta em relação aos elementos já ordenados. Ou seja, é um algoritmo que não realiza trocas, mas sim movimentações (cada troca é composta de 3 movimentações). Um bom exemplo: imagine que você está jogando cartas. Para organizá-las na sua mão, você pega a carta à direita e, a partir da esquerda, encontra seu lugar e a insere ali, não é mesmo? Isso é o insertion sort.
O algoritmo é sensível à ordenação inicial do arquivo: para o pior caso, é O(n²) comparações, mas para o melhor (arquivo ordenado) é O(n). Idem para o número de movimentações.
Caso se tenha um arquivo quase ordenado ou poucos registros para inserir num arquivo ordenado, o insertion sort é mais recomendado do que métodos sofisticados.
Selection Sort: o selection seleciona no conjunto de n elementos o maior (ou menor, dependendo da ordem desejada) e o troca com a primeira posição. A seguir, repete o processo para n-1 elementos. Assim, a cada passada um elemento estará na posição correta.
O número de comparações também é O(n²), porém para cada elemento é feita uma troca (a troca é realizada mesmo se ele já estiver na posição correta). Assim, é O(n) para trocas.
Enumeration Sort: ele percorre o vetor e armazena em outro vetor do mesmo tamanho a posição relativa daquele índice na ordenação. Por exemplo, se tem-se
|9|3|7|4|2|8|, o enumeration cria um outro vetor com os seguintes valores:
|5|1|3|2|0|4|, que correspondem à posição que o elemento de mesmo índice no vetor original ocuparia num vetor ordenado.
Além de não ordenar de fato, o algoritmo ainda ocupa um espaço adicional do tamanho do vetor original, tornando-se extremamente ineficiente.
Bubble Sort: o bubble é um algoritmo baseado em trocas. Ele percorre o vetor do início ao final comparando pares de elementos e trocando-os caso seja necessário. Ele faz isso quantas vezes forem necessárias até que a ordenação esteja completa. A cada passada, o maior elemento analisado já fica no lugar.
O bubble sempre será O(n²) comparações. Para trocas, seu melhor caso é O(1), pois não faz trocas caso os elementos já estejam ordenados, e caso médio e pior caso são O(n²).
É um algoritmo amplamente utilizado didaticamente, porém é ineficiente.
Insertion Sort: o insertion analisa cada elemento e o insere na posição correta em relação aos elementos já ordenados. Ou seja, é um algoritmo que não realiza trocas, mas sim movimentações (cada troca é composta de 3 movimentações). Um bom exemplo: imagine que você está jogando cartas. Para organizá-las na sua mão, você pega a carta à direita e, a partir da esquerda, encontra seu lugar e a insere ali, não é mesmo? Isso é o insertion sort.
O algoritmo é sensível à ordenação inicial do arquivo: para o pior caso, é O(n²) comparações, mas para o melhor (arquivo ordenado) é O(n). Idem para o número de movimentações.
Caso se tenha um arquivo quase ordenado ou poucos registros para inserir num arquivo ordenado, o insertion sort é mais recomendado do que métodos sofisticados.
Selection Sort: o selection seleciona no conjunto de n elementos o maior (ou menor, dependendo da ordem desejada) e o troca com a primeira posição. A seguir, repete o processo para n-1 elementos. Assim, a cada passada um elemento estará na posição correta.
O número de comparações também é O(n²), porém para cada elemento é feita uma troca (a troca é realizada mesmo se ele já estiver na posição correta). Assim, é O(n) para trocas.
Enumeration Sort: ele percorre o vetor e armazena em outro vetor do mesmo tamanho a posição relativa daquele índice na ordenação. Por exemplo, se tem-se
|9|3|7|4|2|8|, o enumeration cria um outro vetor com os seguintes valores:
|5|1|3|2|0|4|, que correspondem à posição que o elemento de mesmo índice no vetor original ocuparia num vetor ordenado.
Além de não ordenar de fato, o algoritmo ainda ocupa um espaço adicional do tamanho do vetor original, tornando-se extremamente ineficiente.
sexta-feira, 26 de julho de 2013
Método de Lagrange
Sejam n+1 pontos (x0, y0), (x1, y1), ..., (xn, yn). Podemos encontrar polinômios interpoladores de modo que o erro seja minimizado. Dado Pi(xi) = 0 e Pj(xj) != 0, temos:
Como o polinômio interpolador não tem grau superior a n, então podemos escrevê-lo como combinação linear. Só que tem um monte de coisas aqui no meu caderno pra ficar escrevendo e substituindo e eu to com preguiça. Vou direto ao trem:
Como o polinômio interpolador não tem grau superior a n, então podemos escrevê-lo como combinação linear. Só que tem um monte de coisas aqui no meu caderno pra ficar escrevendo e substituindo e eu to com preguiça. Vou direto ao trem:
Marcadores:
3º período,
interpolação,
interpolação linear,
interpolação quadrática,
lagrange,
método de lagrange,
métodos numéricos,
metodos-numericos
Interpolação
Dados valores empíricos de uma determinada tabela xi; yi, podemos estimar por um polinômio interpolador valores de xi de modo que tenhamos a variável de resposta yi com certa precisão. O desafio maior para esse caso é exatamente saber qual polinômio utilizar de modo que o erro obtido seja o menor possível.
Interpolação linear
Seja P(x) um polinômio interpolador de modo que P(x) = a0 + a1*x. Deste modo, P(x0) = a0 + a1*x0 = y0 ; P(x1) = a0 + a1*x1 = y1. P(xi) é um polinômio interpolador de grau 1. Para n+1 pontos sempre tem-se (pode-se ter) um polinômio de grau n.
|1 x0| |a0| |y0|
|1 x1| .|a1| = |y1|
Interpolação quadrática
Análogo à interpolação linear, temos que a interpolação quadrática é um polinômio interpolador de grau 2, de modo que P(x0) = a0 + a1*x0 + a2*x0² = y0 ; P(x2) = a0 + a1*x1 + a2*x1² = y1 ; P(x2) = a0 + a1*x2 + a2*x2² = y2. A matriz para a forma quadrática é conhecida como matriz de Vandermonde e seu determinante é não nulo. Isso nos garante que o sistema linear terá uma única solução e o polinômio será único. A matriz:
|1 x0 x0²| |a0| |y0|
|1 x1 x1²| . |a1| = |y1| => o nome disso é preguiça
|1 x2 x2²| |a2| |y2|
Interpolação linear
Seja P(x) um polinômio interpolador de modo que P(x) = a0 + a1*x. Deste modo, P(x0) = a0 + a1*x0 = y0 ; P(x1) = a0 + a1*x1 = y1. P(xi) é um polinômio interpolador de grau 1. Para n+1 pontos sempre tem-se (pode-se ter) um polinômio de grau n.
|1 x0| |a0| |y0|
|1 x1| .|a1| = |y1|
Interpolação quadrática
Análogo à interpolação linear, temos que a interpolação quadrática é um polinômio interpolador de grau 2, de modo que P(x0) = a0 + a1*x0 + a2*x0² = y0 ; P(x2) = a0 + a1*x1 + a2*x1² = y1 ; P(x2) = a0 + a1*x2 + a2*x2² = y2. A matriz para a forma quadrática é conhecida como matriz de Vandermonde e seu determinante é não nulo. Isso nos garante que o sistema linear terá uma única solução e o polinômio será único. A matriz:
|1 x0 x0²| |a0| |y0|
|1 x1 x1²| . |a1| = |y1| => o nome disso é preguiça
|1 x2 x2²| |a2| |y2|
Método de Gauss-Seidel
Seja A uma matriz diagonal estritamente dominante e um valor inicial x0 = bi / aii. A partir do método de Jacobi podemos variar determinados valores de xk de modo que a convergência para os valores de xi ocorram com menor custo. Para isso, é só fazer as contas no mesmo esquema de Jacobi, mas utilizando numa iteração valores obtidos na mesma. Por exemplo, eu descobri o x1. Aí na hora de descobrir o x2, ao invés de usar o x1 da iteração anterior, eu uso o que eu acabei de descobrir. O x3 usa o x2 mais novo e por aí vai. Assim chega mais rapidinho nos resultados!
Novamente, um dia eu posto um exemplo, agora to correndo aqui.
Novamente, um dia eu posto um exemplo, agora to correndo aqui.
Método de Jacobi
Para o método estacionário, devemos decompor A de modo que (D+E+F) = A. Assim, o sistema Ax = b é (D+E+F)x = b. Realizando as operações possíveis, temos Dx = -(E+F)x + b.
Escrevendo x em processo de recorrência (iterativo) temos: xk+1 = -D-1 (E+F)x + D-1b, onde -D-1(E+F)x é uma matriz jacobiana.
A representação em sistema linear matricial, já evidenciando o valor de xi para cada equação linear, é a seguinte:
Escrevendo x em processo de recorrência (iterativo) temos: xk+1 = -D-1 (E+F)x + D-1b, onde -D-1(E+F)x é uma matriz jacobiana.
A representação em sistema linear matricial, já evidenciando o valor de xi para cada equação linear, é a seguinte:
Sendo x0 = bi / aii.
Um dia eu escrevo o exemplo, porque na verdade a prova disso já passou e eu só to atualizando mais ou menos os resumos. Favor me lembrar.
Métodos iterativos estacionários
Um sistema linear pode ser resolvido por um processo iterativo a partir de um valor inicial x0 e uma sequência de vetores {x1, x2, x3 ... xn}.
Critério de parada
Como os métodos são iterativos, eles precisam parar alguma hora, né. Para o critério de parada é definido um valor ɛ tal que
Critério de parada
Como os métodos são iterativos, eles precisam parar alguma hora, né. Para o critério de parada é definido um valor ɛ tal que

Marcadores:
3º período,
estacionários,
iterativos,
iterativos estacionários,
métodos iterativos,
métodos iterativos estacionários,
métodos numéricos,
metodos-numericos
Decomposição por LDLT
Seja A uma matriz simétrica. Podemos decompor A pelo produto de 3 outras matrizes a saber. L é uma matriz triangular inferior e unitária e D é uma matriz diagonal. A solução é: [Ly = b; Dt = y; LTx = t] para 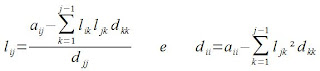 .
.
Podemos ver que um termo usa o outro pra ser definido (l usa d e vice versa). Por isso tem uma ordem para fazer: d11, l21, l31, d22, l32, d33 (num exemplo de matriz de ordem 3). A ordem é essa porque fazendo o d11 (esse é o primeiro em matriz de qualquer ordem) é possível descobrir todos os l da primeira coluna (ou seja, abaixo do índice 11, já que a matriz é triangular inferior e unitária). Após descobrir todos esses, com o d22 dá pra descobrir todos os l abaixo de 22 e por aí vai.
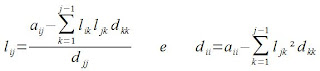 .
.Podemos ver que um termo usa o outro pra ser definido (l usa d e vice versa). Por isso tem uma ordem para fazer: d11, l21, l31, d22, l32, d33 (num exemplo de matriz de ordem 3). A ordem é essa porque fazendo o d11 (esse é o primeiro em matriz de qualquer ordem) é possível descobrir todos os l da primeira coluna (ou seja, abaixo do índice 11, já que a matriz é triangular inferior e unitária). Após descobrir todos esses, com o d22 dá pra descobrir todos os l abaixo de 22 e por aí vai.
quarta-feira, 17 de julho de 2013
Tudo que eu sei pra primeira prova de AOC I
| Aritmética | add | add $s1, $s2, $s3 | $s1 = $s2 + $s3 |
| sub | sub $s1, $s2, $s3 | $s1 = $s2 - $s3 | |
| addi | add $s1, $s2, 100 | $s1 = $s2 + 100 (soma constante) | |
| Transferência de dados | lw | lw $s1, 100($s2) | $s1 = $s2[100] //(Memória[$s2+100] |
| sw | sw $s1, 100($s2) | $s2[100] /*(Memória[$s2+100]<)*/ = $s1 |
foda-se, eu não sei nada
segunda-feira, 15 de julho de 2013
Ordenação
Ordenar é arranjar um conjunto de elementos de acordo com determinada relação. É muito importante para pesquisar e apresentar dados e informação.
Alguns conceitos a serem conhecidos:
Arquivo: é um conjunto de n itens para ser ordenado;
cada Item é um objeto ou registro;
cada Registro contém uma Chave k que governa o processo de ordenação;
podem existir chaves iguais;
Os métodos de ordenação podem ser divididos assim:
Alguns conceitos a serem conhecidos:
Arquivo: é um conjunto de n itens para ser ordenado;
cada Item é um objeto ou registro;
cada Registro contém uma Chave k que governa o processo de ordenação;
podem existir chaves iguais;
Os métodos de ordenação podem ser divididos assim:
Classificação de algoritmos quanto ao método de ordenação:
A ordenação por comparação é quando se observa duas chaves como valores e as compara. É adequada para qualquer tipo de dados e não tem restrições quanto às chaves. Existem quatro tipos de ordenação por comparação:
1) Ordenação por inserção: os itens são considerados um a um e cada novo item é inserido na posição correta relativa aos itens previamente ordenados
2) Ordenação por troca: se dois itens estão fora de ordem, eles são trocados; o processo é repetido até que não sejam necessárias mais trocas
3) Ordenação por seleção: o menor elemento é escolhido e separado dos demais; o processo se repete para os elementos restantes até que reste apenas um elemento
4) Ordenação por enumeração: cada item é comparado com todos os demais; a contagem do número de chaves menores determina a posição relativa do item no conjunto; método exige espaço adicional: não tem interesse prático
A ordenação digital observa os dígitos das chaves separadamente. É mais aconselhada para chaves com um mesmo número de dígitos, ou que seguem uma distribuição uniforme.
Classificação de algoritmos quanto ao espaço requerido pelos métodos:
A ordenação interna é aquela na qual a quantidade de dados cabe na memória principal. O acesso aos dados é mais fácil e pode ser aleatório, permitindo maior flexibilidade na estruturação dos dados.
As operações relevantes para algoritmos internos de comparação são o número de comparações entre chaves, o número de trocas dos elementos e o número de movimentações. O custo varia de acordo com o tamanho do arquivo e o arranjo inicial dos dados. São classificados em
- algoritmos simples (complexidade quadrática): são melhores pra arquivos pequenos. Alguns exemplos são o bubble, insertion, selection e enumeração.
- algoritmos eficientes (complexidade n logn ou n^(3/2)): são mais sofisticados e recomendados para arquivos grandes. Tipo quicksort, shellsort, heapsort, etc.
A ordenação externa é a que os dados não cabem na memória principal, requirindo uso de memória secundária. Há restrições para o acesso dos dados, tornando o acesso sequencial mais rápido do que o aleatório.
Classificação de algoritmos quanto à estabilidade:
Algoritmo estável é aquele que preserva a ordem relativa dos dados. Por exemplo, se pegamos uma lista de clientes de banco e ordenamos primeiro alfabeticamente depois por saldo, os clientes com mesmo saldo permanecem em ordem alfabética - são feitas duas ordenações com chaves diferentes.
A ordenação instável não mantém essa ordem relativa dos dados.
Comparação entre listas estáticas e dinâmicas
Estática
Vantagens● acesso a qualquer elemento com custo O(1), porque os elementos já tem indexação direta
● melhor uso do espaço: só armazena os dados
● não usa apontadores
– implementação mais simples
– menos sujeita a erros
Desvantagens
● custo elevado para inserções e retiradas em qualquer posição: O(n) (porque para inserir numa posição que não seja a última, é preciso deslocar todos os elementos para liberá-la e para retirar, é preciso retornar todos os elementos uma posição)
● redimensionamento é difícil e caro, quando possível - a função realloc() é muito cara.
Dinâmica
Vantagens● alterar o tamanho da lista é simples
● inserção e retirada têm custo O(1) quando é apontado o item a ser retirado
● não necessita deslocar elementos
Desvantagens
● acesso aos elementos é apenas seqüencial
● ocupa mais espaço para armazenar o mesmo número de itens
● uso de apontadores
● implementação mais sujeita a erros
Critérios para a escolha da melhor estrutura
Acesso: como será o acesso aos elementos?
– sempre seqüencial, sempre aleatório?
Número de elementos a ser armazenado
– é conhecido? é previsível? ou não?
Inserções e retiradas
– há muitas inserções e retiradas?
– onde são: no início? no fim? posições variáveis?
Demais operações a serem realizadas
– quais são? busca? máximo ou mínimo?
– pesquisa conjugada com inserção? ordenação eventual ou freqüente?
– retornar o elemento de uma posição específica?
– o custo de todas as operações deve ser analisado em relação a sua freqüência
Espaço ocupado
– há restrições? são muitos dados? dados cabem na memória?
Estruturas de Dados Lineares - Dinâmicas
EDs lineares dinâmicas são implementadas com listas encadeadas. Lista encadeada é aquela cujos elementos possuem apontadores para o próximo elemento (ou pode ter um pro anterior também... enfim, tem ponteiros). Essas listas são ótimas porque podem crescer ou diminuir em tempo de execução, porém a única maneira de acessar os itens é ir seguindo os links entre eles.
A definição de um nodo (célula da lista) é basicamente assim:
struct nodo {
Item item; //pode ser qualquer coisa, meio que não interessa no momento
struct nodo *prox; //note que a definição é recursiva
}
As listas podem ter nodos sentinela, que são células vazias opcionais colocadas no início e/ou fim da lista. Eles não contêm elementos válidos e são usados para simplificar as condições de limites. O nodo final sempre tem o valor null ou 0 ou aponta para um sentinela ou para o início da lista, tornando-a circular.
Implementação de uma lista linear simples com um nodo sentinela
● inicialização
lista = new nodo;
lista->prox = lista;
● testa lista vazia
(lista->prox == lista)
● insere t após x
t->prox = x->prox;
x->prox = t;
● remove nodo após x
t = x->prox;
x->prox = x->prox->prox;
delete t;
● loop para percorrer a lista:
t = lista->prox;
while (t!=lista) {
t->item...; //operação
t = t->prox;
}
A definição de um nodo (célula da lista) é basicamente assim:
struct nodo {
Item item; //pode ser qualquer coisa, meio que não interessa no momento
struct nodo *prox; //note que a definição é recursiva
}
As listas podem ter nodos sentinela, que são células vazias opcionais colocadas no início e/ou fim da lista. Eles não contêm elementos válidos e são usados para simplificar as condições de limites. O nodo final sempre tem o valor null ou 0 ou aponta para um sentinela ou para o início da lista, tornando-a circular.
Implementação de uma lista linear simples com um nodo sentinela
● inicialização
lista = new nodo;
lista->prox = lista;
● testa lista vazia
(lista->prox == lista)
● insere t após x
t->prox = x->prox;
x->prox = t;
● remove nodo após x
t = x->prox;
x->prox = x->prox->prox;
delete t;
● loop para percorrer a lista:
t = lista->prox;
while (t!=lista) {
t->item...; //operação
t = t->prox;
}
Estruturas de Dados Lineares - Estáticas
Uma ED linear estática é implementada por um vetor. Fazem parte da ED: o vetor (dã) e as variáveis de controle (de inserções, retiradas, de quantos elementos tem) - números inteiros representando índices do vetor.
A definição de estrutura vazia pode ser feita via variáveis de controle, sem precisar inspecionar o vetor. Idem para estrutura cheia.
Testes de overflow (erro por tentar inserir elemento na estrutura cheia) e underflow (erro por tentar excluir elemento da estrutura vazia) são essenciais. As posições devem ser verificadas em cada caso de inserção e remoção de elementos.
Exemplo de implementação: pilha
int pilha[MAXTAM]; //a pilha :O
int topo; //a variável de controle, no caso sempre apontando para o topo da pilha
inicializar a pilha:
topo = 0; //inicializa o controle, não o vetor
definir a estrutura vazia
se topo = = 0 então a pilha está vazia
comandos
return topo; //indica o número de elementos da pilha
return (topo = = 0); //indica se a pilha está vazia
verificar se a estrutura está cheia
se (topo = = MAXTAM) então a pilha está cheia
empilhar
se a pilha estiver cheia dá erro de overflow, senão adiciona o elemento no topo e incrementa ele
desempilhar
se a pilha estiver vazia dá erro de underflow, senão decrementa o topo e retira o elemento dele
A definição de estrutura vazia pode ser feita via variáveis de controle, sem precisar inspecionar o vetor. Idem para estrutura cheia.
Testes de overflow (erro por tentar inserir elemento na estrutura cheia) e underflow (erro por tentar excluir elemento da estrutura vazia) são essenciais. As posições devem ser verificadas em cada caso de inserção e remoção de elementos.
Exemplo de implementação: pilha
int pilha[MAXTAM]; //a pilha :O
int topo; //a variável de controle, no caso sempre apontando para o topo da pilha
inicializar a pilha:
topo = 0; //inicializa o controle, não o vetor
definir a estrutura vazia
se topo = = 0 então a pilha está vazia
comandos
return topo; //indica o número de elementos da pilha
return (topo = = 0); //indica se a pilha está vazia
verificar se a estrutura está cheia
se (topo = = MAXTAM) então a pilha está cheia
empilhar
se a pilha estiver cheia dá erro de overflow, senão adiciona o elemento no topo e incrementa ele
desempilhar
se a pilha estiver vazia dá erro de underflow, senão decrementa o topo e retira o elemento dele
Tipos Abstratos de Dados
TADs são especificações de um certo conjunto de dados e das operações possíveis sobre eles, sendo esse conjunto de operações definido de acordo com a aplicação / contexto do problema a ser resolvido. O TAD não inclui a implementação, apenas especificações.
TADs servem para formalizar a definição do tipo de dados e operações. Ele é feito sem conexão com a implementação, permitindo diferentes implementações e que cada parte seja implementada independendo das outras. Um TAD bem implementado pode permitir que a implementação seja alterada mantendo a especificação.
Exemplo de TAD: fila
Modelo matemático: lista: seqüência de elementos
Operações: algoritmos que alteram o conjunto de dados
inicializar a fila: criar uma fila vazia
verificar se a fila está vazia
inserir um elemento na fila
enfileirar: sempre na última posição enqueue
retirar um elemento da fila
desenfileirar: retira o primeiro dequeue
consultar o elemento do início da fila
informar o tamanho da fila: retornar o número de elementos
imprimir a fila
TADs servem para formalizar a definição do tipo de dados e operações. Ele é feito sem conexão com a implementação, permitindo diferentes implementações e que cada parte seja implementada independendo das outras. Um TAD bem implementado pode permitir que a implementação seja alterada mantendo a especificação.
Exemplo de TAD: fila
Modelo matemático: lista: seqüência de elementos
Operações: algoritmos que alteram o conjunto de dados
inicializar a fila: criar uma fila vazia
verificar se a fila está vazia
inserir um elemento na fila
enfileirar: sempre na última posição enqueue
retirar um elemento da fila
desenfileirar: retira o primeiro dequeue
consultar o elemento do início da fila
informar o tamanho da fila: retornar o número de elementos
imprimir a fila
Estruturas de Dados lineares
Estruturas de dados são construções de dados que podem ser implementadas por uma linguagem de programação. Aprender a projetar EDs genéricas e eficientes é importante para saber escolher a certa para usar no programa: a escolha da ED afeta os algoritmos que podem ser utilizados, sendo mais ou menos eficientes, e para os mesmos dados, a ED pode ocupar mais ou menos espaço.
Nesse período serão estudadas EDs lineares: pilhas, filas e listas.
Definição formal de lista:
seqüência linear de 0 ou mais itens ou elementos cuja principal propriedade estrutural é a posição relativa dos elementos na seqüência:
xi precede xi+1 para 1 <= i <= n - 1;
xi sucede xi-1 para 2 <= i <= n;
xi é o i-ésimo elemento da lista, x1 é o primeiro e xn é o último, sendo n o número de elementos (tamanho da lista).
Alguns tipos de listas:
FIFO: First In First Out - o primeiro a entrar é o primeiro a sair
LIFO: Last In First Out - o último a entrar é o primeiro a sair
LRU: Least Recently Used - ordem dos menos utilizados recentemente
MRU: Most Recently Used - ordem dos mais utilizados recentemente
LFU: Least Frequently Used - ordem dos menos frequentemente utilizados
MFU: Most Frequently Used - ordem dos mais frequentemente utilizados
Pilhas e filas são variações de listas. Por exemplo, uma lista FIFO funciona como uma fila e uma LIFO, como uma pilha.
Alocação estática e dinâmica de memória:
Alocação estática de memória é gerenciada pelo compilador e alocada na stack memory. Quando você declara um vetor, por exemplo, ele tem o tamanho definido (no programa ou em tempo de execução, mas é sempre AQUELE tamanho) e já é alocado num espacinho contínuo quando seu programa compila. O acesso a cada elemento do vetor é aleatório e tem mesmo custo: basta ir ao vetor[indice] e pronto.
Alocação dinâmica de memória é gerenciada pelo programador e alocada na parte da memória denominada dynamic heap. Por exemplo: numa lista encadeada, não há um número fixo de elementos. O tamanho da lista é limitado apenas pela memória (heap e virtual), sendo, assim, uma estrutura muito versátil. Portanto, a criação E EXCLUSÃO deles deve ser pensada por você. Lembrando que é muito importante excluir elementos "inúteis" senão eles ficam ocupando memória e não são apagados quando seu programa é fechado. O acesso aos elementos da lista encadeada tem custo diferente para cada um, pois é sequencial. Então, se o elemento buscado for o último, a lista vai ter que ser percorrida inteira, cada elemento apontando para o próximo, até chegar no desejado.
Listas estáticas são implementadas com vetores (coleção fixa de elementos do mesmo tipo armazenados de forma contígua e acessíveis por um índice que têm correspondência direta e sequencial com a memória)
Listas dinâmicas, ligadas ou encadeadas são implementadas com ponteiros. Para entender isso basta ir ao resuminho de PC 1!
Nesse período serão estudadas EDs lineares: pilhas, filas e listas.
Definição formal de lista:
seqüência linear de 0 ou mais itens ou elementos cuja principal propriedade estrutural é a posição relativa dos elementos na seqüência:
xi precede xi+1 para 1 <= i <= n - 1;
xi sucede xi-1 para 2 <= i <= n;
xi é o i-ésimo elemento da lista, x1 é o primeiro e xn é o último, sendo n o número de elementos (tamanho da lista).
Alguns tipos de listas:
FIFO: First In First Out - o primeiro a entrar é o primeiro a sair
LIFO: Last In First Out - o último a entrar é o primeiro a sair
LRU: Least Recently Used - ordem dos menos utilizados recentemente
MRU: Most Recently Used - ordem dos mais utilizados recentemente
LFU: Least Frequently Used - ordem dos menos frequentemente utilizados
MFU: Most Frequently Used - ordem dos mais frequentemente utilizados
Pilhas e filas são variações de listas. Por exemplo, uma lista FIFO funciona como uma fila e uma LIFO, como uma pilha.
Alocação estática e dinâmica de memória:
Alocação estática de memória é gerenciada pelo compilador e alocada na stack memory. Quando você declara um vetor, por exemplo, ele tem o tamanho definido (no programa ou em tempo de execução, mas é sempre AQUELE tamanho) e já é alocado num espacinho contínuo quando seu programa compila. O acesso a cada elemento do vetor é aleatório e tem mesmo custo: basta ir ao vetor[indice] e pronto.
Alocação dinâmica de memória é gerenciada pelo programador e alocada na parte da memória denominada dynamic heap. Por exemplo: numa lista encadeada, não há um número fixo de elementos. O tamanho da lista é limitado apenas pela memória (heap e virtual), sendo, assim, uma estrutura muito versátil. Portanto, a criação E EXCLUSÃO deles deve ser pensada por você. Lembrando que é muito importante excluir elementos "inúteis" senão eles ficam ocupando memória e não são apagados quando seu programa é fechado. O acesso aos elementos da lista encadeada tem custo diferente para cada um, pois é sequencial. Então, se o elemento buscado for o último, a lista vai ter que ser percorrida inteira, cada elemento apontando para o próximo, até chegar no desejado.
Listas estáticas são implementadas com vetores (coleção fixa de elementos do mesmo tipo armazenados de forma contígua e acessíveis por um índice que têm correspondência direta e sequencial com a memória)
Listas dinâmicas, ligadas ou encadeadas são implementadas com ponteiros. Para entender isso basta ir ao resuminho de PC 1!
domingo, 14 de julho de 2013
Capacitância
Um capacitor é um negocinho que armazena carga. É composto por duas placas (podem ser de qualquer formato, mas sempre serão chamadas placas) isolantes com cargas +q e -q. A capacitância é definida por q = CV, sendo q a carga e V a ddp entre as placas. A unidade é o Farad = 1 Coulomb / Volt.
Para calcular a capacitância, podemos
Para calcular a capacitância, podemos
- supor que uma carga q foi colocada nas placas
- calcular, então, o campo E gerado por essa carga
- depois, calcular a ddp V entre as placas
- e por fim, jogando na definição q = CV para encontrar o valor.
Há alguns resultados particulares a serem considerados:
O capacitor de placas paralelas tem capacitância  , sendo A a área das placas e d a distância entre elas.
, sendo A a área das placas e d a distância entre elas.
O capacitor cilíndrico formado por dois cilindros coaxiais longos (comprimento L) e raios a e b tem capacitância .
.
O capacitor esférico formado por duas cascas esféricas concêntricas de raios a e b tem capacitância . Fazendo b = ∞ e a = R, temos a capacitância de uma esfera isolada de raio R: C = 4πɛ0R.
. Fazendo b = ∞ e a = R, temos a capacitância de uma esfera isolada de raio R: C = 4πɛ0R.
Quando se tem capacitores em paralelo ou em série, é possível calcular a capacitância equivalente Ceq pelas seguintes expressões respectivamente: . Quando os capacitores estão em paralelo, todos estão sujeitos à mesma ddp. Em série, a soma das ddps resulta a total.
. Quando os capacitores estão em paralelo, todos estão sujeitos à mesma ddp. Em série, a soma das ddps resulta a total.
A energia potencial elétrica U de um capacitor carregado é igual ao trabalho necessário para carregar o capacitor e pode ser dada pelas seguintes fórmulas: . Essa energia pode ser associada ao campo E entre as placas e, por extensão, podemos associar a qualquer campo elétrico uma energia armazenada. No vácuo, a densidade de energia u (energia potencial por unidade de volume) associada a um campo de módulo E vale
. Essa energia pode ser associada ao campo E entre as placas e, por extensão, podemos associar a qualquer campo elétrico uma energia armazenada. No vácuo, a densidade de energia u (energia potencial por unidade de volume) associada a um campo de módulo E vale  .
.
Agora dica amiga pra quem é aluno do infeliz do meu professor e vai fazer prova amanhã, tipo eu:
Fórmulas que não precisam de dedução:
V =-w/q
e = f/q = kq/d²
q = cv
f = k.q1.q2 / d²
O capacitor cilíndrico formado por dois cilindros coaxiais longos (comprimento L) e raios a e b tem capacitância
O capacitor esférico formado por duas cascas esféricas concêntricas de raios a e b tem capacitância
Quando se tem capacitores em paralelo ou em série, é possível calcular a capacitância equivalente Ceq pelas seguintes expressões respectivamente:
A energia potencial elétrica U de um capacitor carregado é igual ao trabalho necessário para carregar o capacitor e pode ser dada pelas seguintes fórmulas:
Agora dica amiga pra quem é aluno do infeliz do meu professor e vai fazer prova amanhã, tipo eu:
Fórmulas que não precisam de dedução:
V =-w/q
e = f/q = kq/d²
q = cv
f = k.q1.q2 / d²
sexta-feira, 12 de julho de 2013
Potencial elétrico
A variação da energia potencial elétrica U de uma carga que se desloca de um ponto inicial i para um ponto final f é dada por ΔU = Ui - Uf = -W, onde W∞ é o trabalho realizado pela força elétrica no deslocamento da carga de i para f. Se a energia potencial é definida como 0 no infinito, então a energia potencial elétrica U da carga pontual em qualquer ponto é dada por U = -W∞ onde W∞ é o trabalho da força elétrica para trazer a carga do infinito para o ponto em questão.
A diferença de potencial elétrico ΔV entre dois pontos i e f na presença de um campo elétrico é dada por ΔV = Vi - Vf = -W / q, onde q é a carga da partícula na qual é realizado o trabalho. O potencial em um ponto é dado por V = -W∞ / q. A unidade é o Volt = 1 Joule / Coulomb. O potencial também pode ser dado em função da energia potencial U: V = U / q e ΔV = ΔU / q.
Superfícies equipotenciais são pontos que possuem o mesmo potencial elétrico. O trabalho de deslocar uma carga de uma superfície equipotencial para outra não depende dos pontos de início e fim nem da trajetória entre os pontos. O campo elétrico é sempre perpendicular à superfície equipotencial correspondente.
A DDP calculada em função do campo E entre os pontos i e f é dada por , sendo que a integral de linha é calculada ao longo do caminho de i até f.
, sendo que a integral de linha é calculada ao longo do caminho de i até f.
O potencial produzido por uma carga pontual q, a uma distância r da carga, é dado por V = k q / r, e V tem o sinal de q. O potencial produzido por um conjunto de cargas é dado pela somatória dos potenciais de cada uma, ou seja, V = .
.
O potencial produzido por um dipolo elétrico a uma distância r do dipolo e com momento dipolar p = qd (sendo r >> d) é dado por , sendo θ o ângulo entre a reta que liga o ponto ao centro do dipolo e o eixo do dipolo.
, sendo θ o ângulo entre a reta que liga o ponto ao centro do dipolo e o eixo do dipolo.
O potencial produzido por uma distribuição contínua de cargas é dado por onde a integral é calculada para toda a distribuição. Esse dq é distância vezes carga.
onde a integral é calculada para toda a distribuição. Esse dq é distância vezes carga.
Para calcular o campo elétrico E a partir de V, considera-se que a componente de E em qualquer direção é o negativo da taxa de variação com a distância na tal direção. Ou seja, . As componentes de E são
. As componentes de E são  . Caso o campo seja uniforme, ele se reduz a
. Caso o campo seja uniforme, ele se reduz a  , em que s é a direção perpendicular às superfícies equipotenciais. A componente paralela às superfícies é 0.
, em que s é a direção perpendicular às superfícies equipotenciais. A componente paralela às superfícies é 0.
A energia potencial elétrica de um sistema de cargas pontuais é igual ao trabalho de montar esse sistema considerando que as cargas estavam no infinito em repouso. Para duas cargas separadas por uma distância r, a fórmula é a seguinte: . Para mais de duas cargas é só somar a energia dos pares de cargas, um de cada vez.
. Para mais de duas cargas é só somar a energia dos pares de cargas, um de cada vez.
Em equilíbrio, toda carga em excesso de um condutor está na superfície externa dele. A carga se distribui de forma que o potencial de um condutor carregado é o mesmo em todos os pontos do condutor.
A diferença de potencial elétrico ΔV entre dois pontos i e f na presença de um campo elétrico é dada por ΔV = Vi - Vf = -W / q, onde q é a carga da partícula na qual é realizado o trabalho. O potencial em um ponto é dado por V = -W∞ / q. A unidade é o Volt = 1 Joule / Coulomb. O potencial também pode ser dado em função da energia potencial U: V = U / q e ΔV = ΔU / q.
Superfícies equipotenciais são pontos que possuem o mesmo potencial elétrico. O trabalho de deslocar uma carga de uma superfície equipotencial para outra não depende dos pontos de início e fim nem da trajetória entre os pontos. O campo elétrico é sempre perpendicular à superfície equipotencial correspondente.
A DDP calculada em função do campo E entre os pontos i e f é dada por
O potencial produzido por uma carga pontual q, a uma distância r da carga, é dado por V = k q / r, e V tem o sinal de q. O potencial produzido por um conjunto de cargas é dado pela somatória dos potenciais de cada uma, ou seja, V =
 .
.O potencial produzido por um dipolo elétrico a uma distância r do dipolo e com momento dipolar p = qd (sendo r >> d) é dado por
O potencial produzido por uma distribuição contínua de cargas é dado por
Para calcular o campo elétrico E a partir de V, considera-se que a componente de E em qualquer direção é o negativo da taxa de variação com a distância na tal direção. Ou seja,
 . Caso o campo seja uniforme, ele se reduz a
. Caso o campo seja uniforme, ele se reduz a  , em que s é a direção perpendicular às superfícies equipotenciais. A componente paralela às superfícies é 0.
, em que s é a direção perpendicular às superfícies equipotenciais. A componente paralela às superfícies é 0.A energia potencial elétrica de um sistema de cargas pontuais é igual ao trabalho de montar esse sistema considerando que as cargas estavam no infinito em repouso. Para duas cargas separadas por uma distância r, a fórmula é a seguinte:
Em equilíbrio, toda carga em excesso de um condutor está na superfície externa dele. A carga se distribui de forma que o potencial de um condutor carregado é o mesmo em todos os pontos do condutor.
sábado, 6 de julho de 2013
Lei de Gauss
Uma superfície gaussiana é uma superfície imaginária fechada que envolve a distribuição de cargas de um objeto. Ela pode ter qualquer forma, mas se possuir alguma simetria na distribuição de cargas os cálculos ficam mais fáceis.
A lei de Gauss relaciona os campos elétricos nos pontos de uma superfície gaussiana à carga total envolvida pela superfície. É expressa por .
.
O fluxo do campo elétrico através de uma superfície gaussiana é dado por . O vetor A representa a área que se está analisando. Ele tem o módulo da área e é perpendicular a ela.
. O vetor A representa a área que se está analisando. Ele tem o módulo da área e é perpendicular a ela.
É possível demonstrar, usando a lei de Gauss, que:
A lei de Gauss relaciona os campos elétricos nos pontos de uma superfície gaussiana à carga total envolvida pela superfície. É expressa por
O fluxo do campo elétrico através de uma superfície gaussiana é dado por
É possível demonstrar, usando a lei de Gauss, que:
- Cargas em excesso de um condutor se concentram na superfície externa deste;
- O campo elétrico externo nas proximidades da superfície de um condutor carregado é perpendicular à superfície e tem módulo
, sendo sigma a densidade superficial de cargas. Dentro do condutor, o campo é 0;
- O campo elétrico em qualquer ponto de uma linha de cargas infinita e com densidade linear de cargas uniforme lambda é perpendicular à linha e tem módulo
, sendo r a distância entre a linha e o ponto em que se está analisando;
- O campo elétrico produzido por uma placa não-condutora infinita com uma densidade superficial de cargas uniforme sigma é perpendicular ao plano da placa e tem módulo
;
- O campo elétrico no exterior de uma casca esférica uniformemente carregada de raio R e carga q aponta na direção radial e tem módulo
, sendo r a distância entre o ponto analisado e a casca. A carga se comporta como se estivesse concentrada no centro da esfera. O campo dentro da casca é 0;
- O campo elétrico no interior de uma esfera uniformemente carregada aponta na direção radial e tem módulo
.
segunda-feira, 10 de junho de 2013
Recursão e análise de algoritmos recursivos
O algoritmo recursivo é aquele que referencia a si mesmo, direta ou indiretamente. Quem chegou até aqui já está cansado de saber disso, já que a recursão é introduzida em PC I.
Dentre os aspectos importantes do algoritmo recursivo está a condição de terminação: sem ela, o algoritmo entra em loop infinito.
Exemplo de uma função recursiva:
long fatorial(int n) {
if ((n == 0) || (n == 1)) // condição de terminação
return 1;
else // caso recursivo
return (n * fatorial(n -1));
}
Observe que a função retorna uma chamada dela mesma com um valor uma unidade menor do que a "origem" da chamada até que este valor seja 0 ou 1.
Durante a execução de um algoritmo recursivo, vão sendo abertas novas chamadas da função conforme o tempo de execução aumenta. Portanto, o número máximo de chamadas abertas é um fator importante a ser considerado ao programar recursivamente. No exemplo do fatorial de n, n chamadas ficam empilhadas na pilha de recursão, pois cada uma espera o resultado da anterior para calcular e retornar um valor.
A recursão nunca deve ser utilizada no lugar de um laço simples. Se a chamada recursiva vier no início ou no fim do código, provavelmente pode ser substituída com facilidade por um laço.
O tempo de execução de um algoritmo recursivo é expresso por uma relação de recorrência, que é uma equação ou inequação que descreve uma função em termos de seus valores sobre entradas menores. É composta pelo caso base (conhecido) e pelo caso indutivo, que é deduzido a partir dos casos anteriores. Exemplo:
Dentre os aspectos importantes do algoritmo recursivo está a condição de terminação: sem ela, o algoritmo entra em loop infinito.
Exemplo de uma função recursiva:
long fatorial(int n) {
if ((n == 0) || (n == 1)) // condição de terminação
return 1;
else // caso recursivo
return (n * fatorial(n -1));
}
Observe que a função retorna uma chamada dela mesma com um valor uma unidade menor do que a "origem" da chamada até que este valor seja 0 ou 1.
Durante a execução de um algoritmo recursivo, vão sendo abertas novas chamadas da função conforme o tempo de execução aumenta. Portanto, o número máximo de chamadas abertas é um fator importante a ser considerado ao programar recursivamente. No exemplo do fatorial de n, n chamadas ficam empilhadas na pilha de recursão, pois cada uma espera o resultado da anterior para calcular e retornar um valor.
A recursão nunca deve ser utilizada no lugar de um laço simples. Se a chamada recursiva vier no início ou no fim do código, provavelmente pode ser substituída com facilidade por um laço.
O tempo de execução de um algoritmo recursivo é expresso por uma relação de recorrência, que é uma equação ou inequação que descreve uma função em termos de seus valores sobre entradas menores. É composta pelo caso base (conhecido) e pelo caso indutivo, que é deduzido a partir dos casos anteriores. Exemplo:
A partir da fórmula tem-se
tem-se
 tem-se
tem-se
Há o caso base (T(1) = 1) e a fórmula para descobrir um padrão.
domingo, 9 de junho de 2013
Exercícios resolvidos - Complexidade assintótica
Utilizando as definições para as notações assintóticas, prove se são verdadeiras ou falsas as seguintes afirmativas:
1) 3n³ + 2n² + n + 1 = O(n³)
3n³ + 2n² + n + 1 <= c * n³
3 + 2/n + 1/n² + 1 <= c
menor valor possível de c: 3 + 2 + 1 + 1 = 7
verdadeira para c = 7 e n0 = 1
2) 7n² = O(n)
7n² <= c * n
7n <= c
não existe um valor para c que seja sempre maior que n, portanto a afirmação é falsa
3) 2n+2 = O(2n)
2n+2 <= c * 2n
2n * 22<= c * 2n
2² <= c
verdadeira para n0 = 1 e c = 4
4)22n = O(2n)
(2n)² <= c * 2n
2n <= cnão existe um valor para c que seja sempre maior que n, portanto a afirmação é falsa
5) 5n² + 7n = Θ(n²)
5n² + 7n <= c2 * n² c1 * n² <= 5n² + 7n
5 + 7/n <= c2 c1 <= 5 + 7/n
5 + 7/1 <= c2 c1 <= 5 + 7/infinito
verdadeiro para n0 = 1, c1 = 5 e c2 = 12
no cálculo de c1, considera-se n0 tendendo ao infinito fazendo 7/n assumir o menor valor possível; já no cálculo de c2, considera-se n0 = 1 para que 7/n assuma o maior valor possível.
6) 6n³ + 5n² ≠ Θ(n²)
c1 * n² <= 6n³ + 5n² 6n³ + 5n² <= c2 * n²
c1 <= 6n + 5 6n + 5 <= c2
para n0 = 1, c1 pode valer 11. Porém, não existe um valor fixo para c2. Portanto, a afirmativa é VERDADEIRA, pois perguntava se a expressão era DIFERENTE de Θ(n²).
7) 9n³ + 3n = Ω(n)
9n³ + 3n >= c * n
9n² + 3 >= c
verdadeira para n0 = 1 e c = 12.
Obs: nem sempre n0 precisa ser 1. Vários pares (ou triplas) de valores podem resolver as expressões.
1) 3n³ + 2n² + n + 1 = O(n³)
3n³ + 2n² + n + 1 <= c * n³
3 + 2/n + 1/n² + 1 <= c
menor valor possível de c: 3 + 2 + 1 + 1 = 7
verdadeira para c = 7 e n0 = 1
2) 7n² = O(n)
7n² <= c * n
7n <= c
não existe um valor para c que seja sempre maior que n, portanto a afirmação é falsa
3) 2n+2 = O(2n)
2n+2 <= c * 2n
2n * 22<= c * 2n
2² <= c
verdadeira para n0 = 1 e c = 4
4)22n = O(2n)
(2n)² <= c * 2n
2n <= cnão existe um valor para c que seja sempre maior que n, portanto a afirmação é falsa
5) 5n² + 7n = Θ(n²)
5n² + 7n <= c2 * n² c1 * n² <= 5n² + 7n
5 + 7/n <= c2 c1 <= 5 + 7/n
5 + 7/1 <= c2 c1 <= 5 + 7/infinito
verdadeiro para n0 = 1, c1 = 5 e c2 = 12
no cálculo de c1, considera-se n0 tendendo ao infinito fazendo 7/n assumir o menor valor possível; já no cálculo de c2, considera-se n0 = 1 para que 7/n assuma o maior valor possível.
6) 6n³ + 5n² ≠ Θ(n²)
c1 * n² <= 6n³ + 5n² 6n³ + 5n² <= c2 * n²
c1 <= 6n + 5 6n + 5 <= c2
para n0 = 1, c1 pode valer 11. Porém, não existe um valor fixo para c2. Portanto, a afirmativa é VERDADEIRA, pois perguntava se a expressão era DIFERENTE de Θ(n²).
7) 9n³ + 3n = Ω(n)
9n³ + 3n >= c * n
9n² + 3 >= c
verdadeira para n0 = 1 e c = 12.
Obs: nem sempre n0 precisa ser 1. Vários pares (ou triplas) de valores podem resolver as expressões.
Assinar:
Comentários (Atom)

















